!pip install transformers==4.2.1
!pip install sentencepiece==0.1.95Vaswani 等人在其名作 Attention is all you need 中首创了 基于 transformer 的编码器-解码器模型,如今已成为自然语言处理 (natural language processing,NLP) 领域编码器-解码器架构的 事实标准 。
最近基于 transformer 的编码器-解码器模型训练这一方向涌现出了大量关于 预训练目标函数 的研究, 例如 T5、Bart、Pegasus、ProphetNet、Marge 等,但它们所使用的网络结构并没有改变。
本文的目的是 详细 解释如何用基于 transformer 的编码器-解码器架构来对 序列到序列 (sequence-to-sequence) 问题进行建模。我们将重点关注有关这一架构的数学知识以及如何对该架构的模型进行推理。在此过程中,我们还将介绍 NLP 中序列到序列模型的一些背景知识,并将 基于 transformer 的编码器-解码器架构分解为 编码器 和 解码器 这两个部分分别讨论。我们提供了许多图例,并把 基于 transformer 的编码器-解码器模型的理论与其在 🤗 transformers 推理场景中的实际应用二者联系起来。请注意,这篇博文 不 解释如何训练这些模型 —— 我们会在后续博文中涵盖这一方面的内容。
基于 transformer 的编码器-解码器模型是 表征学习 和 模型架构 这两个领域多年研究成果的结晶。本文简要介绍了神经编码器-解码器模型的历史,更多背景知识,建议读者阅读由 Sebastion Ruder 撰写的这篇精彩 博文。此外,建议读者对 自注意力 (self-attention) 架构 有一个基本了解,可以阅读 Jay Alammar 的 这篇博文 复习一下原始 transformer 模型。
截至本文撰写时,🤗 transformers 库已经支持的编码器-解码器模型有: T5 、 Bart 、 MarianMT 以及 Pegasus ,你可以从 这儿 获取相关信息。
本文分 4 个部分:
- 背景 – 简要回顾了神经编码器-解码器模型的历史,重点关注基于 RNN 的模型。
- 编码器-解码器 – 阐述基于 transformer 的编码器-解码器模型,并阐述如何使用该模型进行推理。
- 编码器 – 阐述模型的编码器部分。
- 解码器 – 阐述模型的解码器部分。
每个部分都建立在前一部分的基础上,但也可以单独阅读。
背景
自然语言生成 (natural language generation,NLG) 是 NLP 的一个子领域,其任务一般可被建模为序列到序列问题。这类任务可以定义为寻找一个模型,该模型将输入词序列映射为目标词序列,典型的例子有 摘要 和 翻译 。在下文中,我们假设每个单词都被编码为一个向量表征。因此,$n$ 个输入词可以表示为 $n$ 个输入向量组成的序列:
$$
\mathbf{X}_{1:n} = {\mathbf{x}_1, \ldots, \mathbf{x}_n}
$$
因此,序列到序列问题可以表示为找到一个映射 $f$,其输入为 $n$ 个向量的序列,输出为 $m$ 个向量的目标序列 $\mathbf{Y}_{1:m}$。这里,目标向量数 $m$ 是先验未知的,其值取决于输入序列:
$$ f: \mathbf{X}{1:n} \to \mathbf{Y}{1:m} $$
Sutskever 等 (2014) 的工作指出,深度神经网络 (deep neural networks,DNN)“ 尽管灵活且强大,但只能用于拟合输入和输出维度均固定的映射。 ” ${}^1$
因此,要用使用 DNN 模型 ${}^2$ 解决序列到序列问题就意味着目标向量数 $m$ 必须是先验已知的,且必须独立于输入 $\mathbf{X}{1:n}$。这样设定肯定不是最优的。因为对 NLG 任务而言,目标词的数量通常取决于输入内容 $\mathbf{X}{1:n}$,而不仅仅是输入长度 $n$。 例如 ,一篇 1000 字的文章,根据内容的不同,有可能可以概括为 200 字,也有可能可以概括为 100 字。
2014 年,Cho 等人 和 Sutskever 等人 提出使用完全基于递归神经网络 (recurrent neural networks,RNN) 的编码器-解码器模型来解决 序列到序列 任务。与 DNN 相比,RNN 支持输出可变数量的目标向量。下面,我们深入了解一下基于 RNN 的编码器-解码器模型的功能。
在推理过程中,RNN 编码器通过连续更新其 隐含状态 ${}^3$ 对输入序列 $\mathbf{X}_{1:n}$ 进行编码。我们定义处理完最后一个输入向量 $\mathbf{x}_n$ 后的编码器隐含状态为 $\mathbf{c}$。因此,编码器主要完成如下映射:
$$ f{\theta{enc}}: \mathbf{X}_{1:n} \to \mathbf{c}
$$
然后,我们用 $\mathbf{c}$ 来初始化解码器的隐含状态,再用解码器 RNN 自回归地生成目标序列。
下面,我们进一步解释一下。从数学角度讲,解码器定义了给定隐含状态 $\mathbf{c}$ 下目标序列 $\mathbf{Y}_{1:m}$ 的概率分布:
$$ p{\theta{dec}}(\mathbf{Y}_{1:m} |\mathbf{c})
$$
根据贝叶斯法则,上述分布可以分解为每个目标向量的条件分布的积,如下所示:
$$ p{\theta{dec}}(\mathbf{Y}{1:m} |\mathbf{c}) = \prod{i=1}^{m} p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})
$$
因此,如果模型架构可以在给定所有前驱目标向量的条件下对下一个目标向量的条件分布进行建模的话:
$$ p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c}), \forall i \in {1, \ldots, m}
$$
那它就可以通过简单地将所有条件概率相乘来模拟给定隐藏状态 $\mathbf{c}$ 下任意目标向量序列的分布。
那么基于 RNN 的解码器架构如何建模
$p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$ 呢?
从计算角度讲,模型按序将前一时刻的内部隐含状态 $\mathbf{c}{i-1}$ 和前一时刻的目标向量 $\mathbf{y}{i-1}$ 映射到当前内部隐含状态 $\mathbf{c}_i$ 和一个 logit 向量 $\mathbf{l}_i$ (下图中以深红色表示):
$$ f{\theta{\text{dec}}}(\mathbf{y}{i-1}, \mathbf{c}{i-1}) \to \mathbf{l}_i, \mathbf{c}_i
$$
此处,$\mathbf{c}_0$ 为 RNN 编码器的输出。随后,对 logit 向量 $\mathbf{l}_i$ 进行 softmax 操作,将其变换为下一个目标向量的条件概率分布:
$$ p(\mathbf{y}_i | \mathbf{l}_i) = \textbf{Softmax}(\mathbf{l}_i), \text{ 其中 } \mathbf{l}i = f{\theta{\text{dec}}}(\mathbf{y}{i-1}, \mathbf{c}_{\text{prev}})
$$
更多有关 logit 向量及其生成的概率分布的详细信息,请参阅脚注 ${}^4$。从上式可以看出,目标向量 $\mathbf{y}i$ 的分布是其前一时刻的目标向量 $\mathbf{y}{i-1}$ 及前一时刻的隐含状态 $\mathbf{c}{i-1}$ 的条件分布。而我们知道前一时刻的隐含状态 $\mathbf{c}{i-1}$ 依赖于之前所有的目标向量 $\mathbf{y}0, \ldots, \mathbf{y}{i- 2}$,因此我们可以说 RNN 解码器 隐式 (或间接) 地建模了条件分布
$p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$。
目标向量序列 $\mathbf{Y}{1:m}$ 的概率空间非常大,因此在推理时,必须借助解码方法对 = ${}^5$ 对 $p{\theta{dec}}(\mathbf{Y}{1:m} |\mathbf{c})$ 进行采样才能高效地生成最终的目标向量序列。
给定某解码方法,在推理时,我们首先从分布 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$ 中采样出下一个输出向量; 接着,将其添加至解码器输入序列末尾,让解码器 RNN 继续从
$p{\theta{\text{dec}}}(\mathbf{y}{i+1} | \mathbf{Y}{0: i}, \mathbf{c})$ 中采样出下一个输出向量 $\mathbf{y}_{i+1}$,如此往复,整个模型就以 自回归 的方式生成了最终的输出序列。
基于 RNN 的编码器-解码器模型的一个重要特征是需要定义一些 特殊 向量,如 $\text{EOS}$ (终止符) 和 $\text{BOS}$ (起始符) 向量。 $\text{EOS}$ 向量通常意味着 $\mathbf{x}_n$ 中止,出现这个即“提示”编码器输入序列已结束; 如果它出现在目标序列中意味着输出结束,一旦从 logit 向量中采样到 $\text{EOS}$,生成就完成了。$\text{BOS}$ 向量用于表示在第一步解码时馈送到解码器 RNN 的输入向量 $\mathbf{y}_0$。为了输出第一个 logit $\mathbf{l}_1$,需要一个输入,而由于在其之前还没有生成任何输入,所以我们馈送了一个特殊的 $\text{BOS}$ 输入向量到解码器 RNN。好,有点绕了!我们用一个例子说明一下。
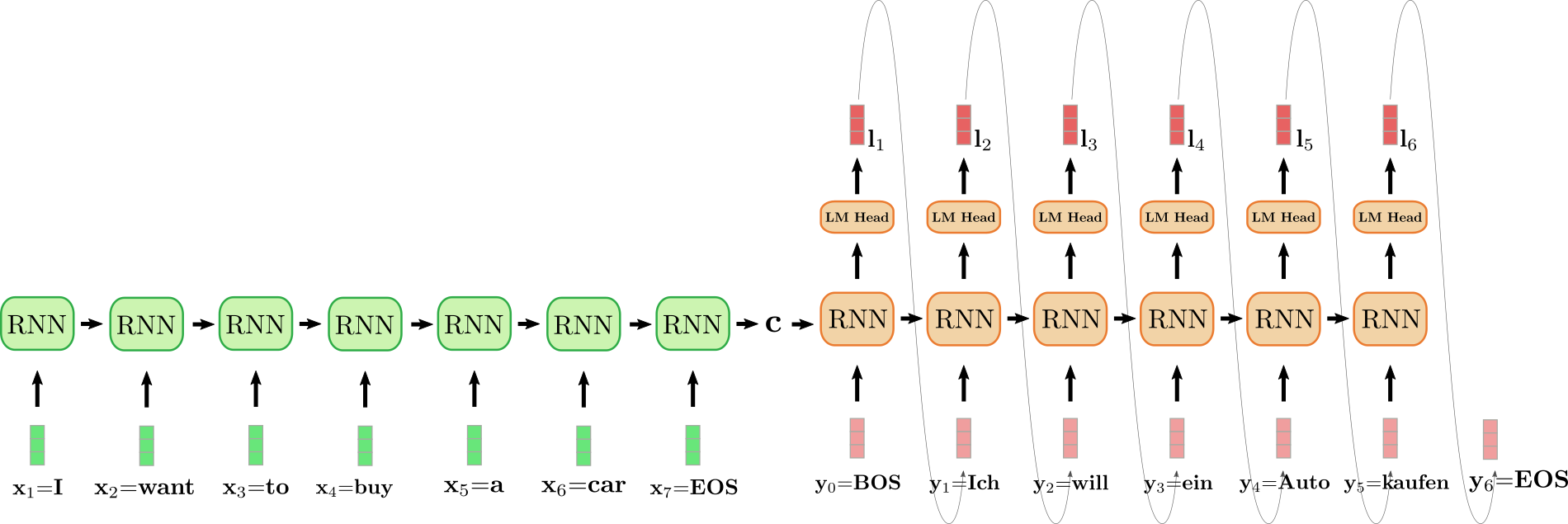
上图中,我们将编码器 RNN 编码器展开,并用绿色表示; 同时,将解码器 RNN 展开,并用红色表示。
英文句子 I want to buy a car,表示为 $(\mathbf{x}_1 = \text{I}$,$\mathbf{x}_2 = \text{want}$,$\mathbf{x}_3 = \text{to}$,$\mathbf{x}_4 = \text{buy}$,$\mathbf{x}_5 = \text{a}$,$\mathbf{x}_6 = \text{car}$,$\mathbf{x}_7 = \text{EOS}$)。将其翻译成德语: “Ich will ein Auto kaufen",表示为 $(\mathbf{y}_0 = \text{BOS}$,$\mathbf{y}_1 = \text{Ich}$,$\mathbf{y}_2 = \text{will}$,$\mathbf{y}_3 = \text {ein}$,$\mathbf{y}_4 = \text{Auto}$,$\mathbf{y}_5 = \text{kaufen}$,$\mathbf{y}_6=\text{EOS}$)。首先,编码器 RNN 处理输入向量 $\mathbf{x}_1 = \text{I}$ 并更新其隐含状态。请注意,对编码器而言,因为我们只对其最终隐含状态 $\mathbf{c}$ 感兴趣,所以我们可以忽略它的目标向量。然后,编码器 RNN 以相同的方式依次处理输入句子的其余部分: $\text{want}$、$\text{to}$、$\text{buy}$、$\text{a}$、$\text{car}$、$\text{EOS}$,并且每一步都更新其隐含状态,直到遇到向量 $\mathbf{x}_7={EOS}$ ${}^6$。在上图中,连接展开的编码器 RNN 的水平箭头表示按序更新隐含状态。编码器 RNN 的最终隐含状态,由 $\mathbf{c}$ 表示,其完全定义了输入序列的 编码 ,并可用作解码器 RNN 的初始隐含状态。可以认为,解码器 RNN 以编码器 RNN 的最终隐含状态为条件。
为了生成第一个目标向量,将 $\text{BOS}$ 向量输入给解码器,即上图中的 $\mathbf{y}_0$。然后通过 语言模型头 (LM Head) 前馈层将 RNN 的目标向量进一步映射到 logit 向量 $\mathbf{l}_1$,此时,可得第一个目标向量的条件分布:
$$ p{\theta{dec}}(\mathbf{y} | \text{BOS}, \mathbf{c})
$$
最终采样出第一个目标词 $\text{Ich}$ (如图中连接 $\mathbf{l}_1$ 和 $\mathbf{y}_1$ 的灰色箭头所示)。接着,继续采样出第二个目标向量:
$$ \text{will} \sim p{\theta{dec}}(\mathbf{y} | \text{BOS}, \text{Ich}, \mathbf{c})
$$
依此类推,一直到第 6 步,此时从 $\mathbf{l}6$ 中采样出 $\text{EOS}$,解码完成。输出目标序列为 $\mathbf{Y}{1:6} = {\mathbf{y}_1, \ldots, \mathbf{y}_6}$, 即上文中的 “Ich will ein Auto kaufen”。
综上所述,我们通过将分布 $p(\mathbf{Y}{1:m} | \mathbf{X}{1:n})$ 分解为 $f{\theta{\text{enc}}}$ 和 $p{\theta{\text{dec}}}$ 的表示来建模基于 RNN 的 encoder-decoder 模型:
$$ p{\theta{\text{enc}}, \theta{\text{dec}}}(\mathbf{Y}{1:m} | \mathbf{X}{1:n}) = \prod{i=1}^{m} p{\theta{\text{enc}}, \theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{X}{1:n}) = \prod{i=1}^{m} p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c}), \text{ 其中 } \mathbf{c}=f{\theta{enc}}(X) $$
在推理过程中,利用高效的解码方法可以自回归地生成目标序列 $\mathbf{Y}_{1:m}$。
基于 RNN 的编码器-解码器模型席卷了 NLG 社区。2016 年,谷歌宣布用基于 RNN 的编码器-解码器单一模型完全取代其原先使用的的含有大量特征工程的翻译服务 (参见
此处)。
然而,基于 RNN 的编码器-解码器模型存在两个主要缺陷。首先,RNN 存在梯度消失问题,因此很难捕获长程依赖性, 参见Hochreiter 等 (2001) 的工作。其次,RNN 固有的循环架构使得在编码时无法进行有效的并行化, 参见Vaswani 等 (2017) 的工作。
${}^1$ 论文的原话是“ 尽管 DNN 具有灵活性和强大的功能,但它们只能应用于输入和目标可以用固定维度的向量进行合理编码的问题 ”,用在本文时稍作调整。
${}^2$ 这同样适用于卷积神经网络 (CNN)。虽然可以将可变长度的输入序列输入 CNN,但目标的维度要么取决于输入维数要么需要固定为特定值。
${}^3$ 在第一步时,隐含状态被初始化为零向量,并与第一个输入向量 $\mathbf{x}_1$ 一起馈送给 RNN。
${}^4$ 神经网络可以将所有单词的概率分布定义为 $p(\mathbf{y} | \mathbf{c}, \mathbf{Y}{0 : i-1})$。首先,其将输入 $\mathbf{c}, \mathbf{Y}{0: i-1}$ 转换为嵌入向量 $\mathbf{y’}$,该向量对应于 RNN 模型的目标向量。随后将 $\mathbf{y’}$ 送给“语言模型头”,即将其乘以 词嵌入矩阵 (即$\mathbf{Y}^{\text{vocab}}$),得到 $\mathbf{y’}$ 和词表 $\mathbf{Y}^{\text{vocab}}$ 中的每个向量 $\mathbf{y}$ 的相似度得分,生成的向量称为 logit 向量 $\mathbf{l} = \mathbf{Y}^{\text{vocab}} \mathbf{y’}$,最后再通过 softmax 操作归一化成所有单词的概率分布: $p(\mathbf{y} | \mathbf{c}) = \text{Softmax}(\mathbf{Y}^{\text{vocab}} \mathbf{y’}) = \text {Softmax}(\mathbf{l})$。
${}^5$ 波束搜索 (beam search) 是其中一种解码方法。本文不会对不同的解码方法进行介绍,如对此感兴趣,建议读者参考 此文。
${}^6$ Sutskever 等 (2014) 的工作对输入顺序进行了逆序,对上面的例子而言,输入向量变成了 ($\mathbf{x}_1 = \text{car}$,$\mathbf{x}_2 = \text{a}$,$\mathbf{x}_3 = \text{buy}$,$\mathbf{x}_4 = \text{to}$,$\mathbf{x}_5 = \text{want}$,$\mathbf{x}_6 = \text{I}$,$\mathbf{x}_7 = \text{EOS}$)。其动机是让对应词对之间的连接更短,如可以使得 $\mathbf{x}_6 = \text{I}$ 和 $\mathbf{y}_1 = \text{Ich}$ 之间的连接更短。该研究小组强调,将输入序列进行逆序是他们的模型在机器翻译上的性能提高的一个关键原因。
敬请关注其余部分的文章。
赞赏英文原文:
https://hf.co/blog/encoder-decoder 原文作者: Patrick von Platen
译者: Matrix Yao (姚伟峰),英特尔深度学习工程师,工作方向为 transformer-family 模型在各模态数据上的应用及大规模模型的训练推理。
审校/排版: zhongdongy (阿东)
 微信赞赏
微信赞赏 支付宝赞赏
支付宝赞赏
相关文章




